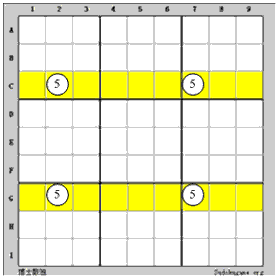
四辺形(二択)の原則/(X-wing)

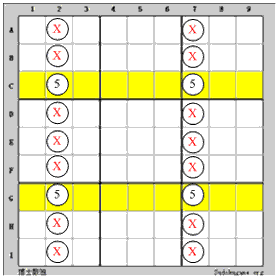上図のように、数字５は行Ｃと行Ｇで強リンク（Strong Link）になる上に、Ｃ２とＧ２は同じ列、Ｃ７とＧ７は同じ列にあります。そうであれば、列２と列７のほかのセルは５であるはずがありません。次のように推論します：

たとえ(C2=5) =>(C7<>5,G2<>5)=>(G7=5)
(C2<>5)=>(C7=5)=>(G7<>5)=>(G2=5)

としたら、（Ｃ２、Ｇ７）が全部５であるか、（Ｇ５、Ｃ７）が全部５であることが分かります。どちらであっても、列２と列７のほかのセルに５を入れてはいけません。

これは四辺形(二択)の原則です。

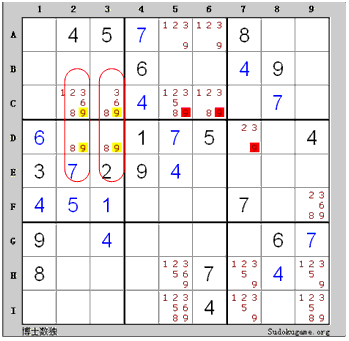
上図に、Ｃ５、Ｃ６、Ｄ７の中にある９は全部削除してもいいです。

四辺形（三択）の原則(Swordfish)

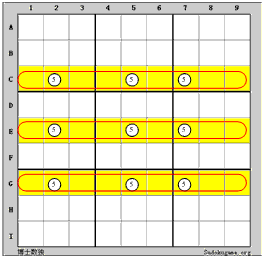
上の「四辺形（二択）の原則」からもっと伸ばします。下図のように：

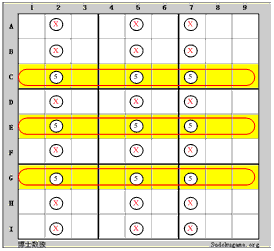数字５はＣ行のＣ２、Ｃ５、Ｃ７だけに現れる

数字５はE行のE２、E５、E７だけに現れる

数字５はＧ行のＧ２、Ｇ５、Ｇ７だけに現れる

そうすれば列２、列５、列７に、ほかのセルにある数字５は全部削除してもいいです。

次のように推論します：

数独のルールによって、行Ｃ、行E、行Ｇに必ず数字５が三個で、別々の列にあります。上図の条件から見れば、数字５は列２、列５、列７に現れる位置は必ずＣ、E、Ｇ行にあるので、列２、列５、列７でほかのセルにある５は全部削除してもいいです。

本図から推論方法が同じで、ちょっと変わる変化図があります。以下は変化図です。

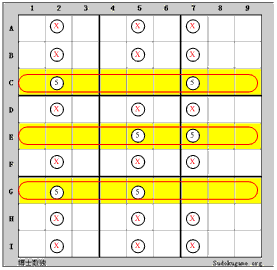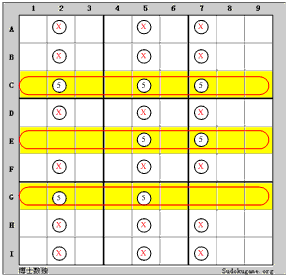（この内容の図は全部博士数独からのです。博士数独は豊かな色付け機能と候補数の表示機能を提供しております。）