数独無料ゲーム

数独の解き方

無料で印刷できる数独

数独問題集

初級 中級 上級

専門級 最高級

数独ソルバー

博士数独

以前の数独

m.sudokugame.org を入れれば、携帯で数独ができます。

DBMover
The best database Converter

ＸＹチェーン(XY-Chain) - 数独の解き方

ＸＹチェーンになるセルの候補数は全部二つしかありません。各セルは同じ数字で繋がり、違うセルに使う数字は違ってもいいです。下図をご覧ください。

（例を数独ソルバーにロード）

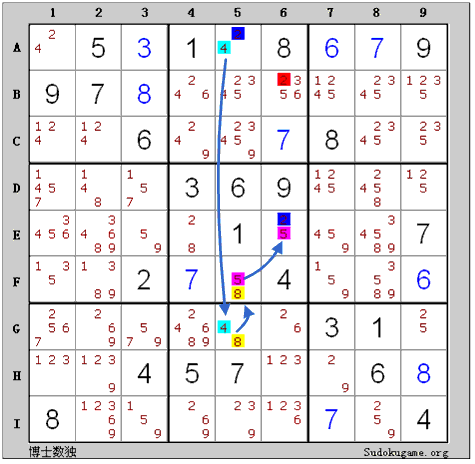
このＸＹチェーンは（A5，G5，F5，E6）四つの点からなります。この四つのセルにも二つの候補数しかありません。（A5，G5）は4で、（G5，F5）は8で、（F5，E6）は5で繋がります。チェーンの両端A5とE6ともに繋がられていない数字が2です。これでＸＹチェーンになります。A5とE6に必ず2がある結論が出て、つまり(A5,E6)と交わるＢ６にある候補数２は削除してもいいです。

次のように推論できます：

A5=2 => B6<>2

A5<>2 => G5=8 => F5=5 => E6=2 => B6<>2

Ａ５は2でなければ、Ｅ６は2です。どちらでもＢ６は必ず2ではないことが分かります。

 

下図をご覧ください。

（例を数独ソルバーにロード）

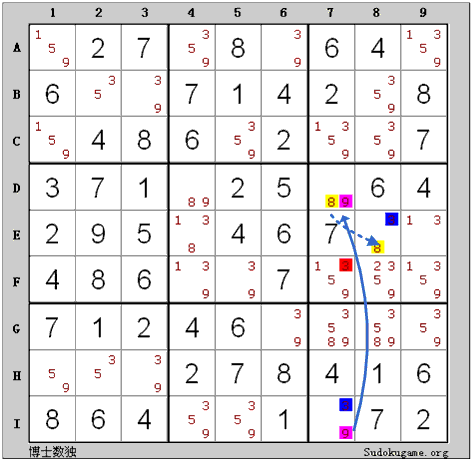
これは一番短いＸＹチェーンです。ＸＹ-Wingの例にも説明しました。　XY-Wingは一番短いＸＹチェーンです。チェーンの両端I7とE8に必ず３があるので、Ｆ７にある候補数3を削除してもいいです。



（この内容の図は全部博士数独からのです。博士数独は豊かな色付け機能と候補数の表示機能を提供しております。）