XY-wing

XY-wingはY-Wingとも言え、候補数を削除するいい方法です。下図をご覧ください。

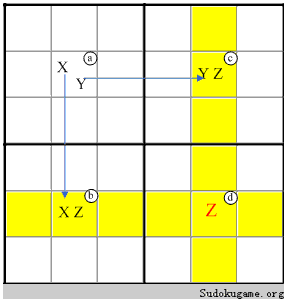
XYZは三つの違う候補数です。この三つの数字から長方形になって、abcdで四つの交差点を表示します。長方形の三つの角は別々に二個の候補数あります（XY，XZ,，YZ）。

ＸＹがあるセルaは問題を解くヒントです。

次のように推論できます：

(a=X) => (b<>X) => (b=Z) => (d<>Z)

(a<>X) => (a=Y) => (c<>Y) => (c=Z) =>(d<>Z)

以上から見れば、aはＸかＹであっても、dにある候補数Ｚは削除できます。

下図をご覧ください：

(ab)(ac)はＸＹ-wingになって、bかcの中必ずＺがあることが推量できます。だからbかcと同じブロックにあるセルの中のＺは全部削除してもいいです。この図にある赤いＺはこれらのセルにＺを入れるはずがないという意味です。

次は一つの実際の例です：

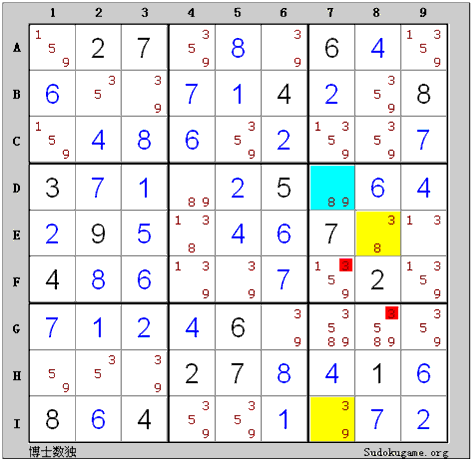
（D7、I7）と（D7、E8）はXY-Wingになるので、I7かE8の中必ず３があります。それでＦ７、Ｇ８の中にある候補数３は削除してもいいです。（例を数独ソルバーにロード）

（この内容の図は全部博士数独からのです。博士数独は豊かな色付け機能と候補数の表示機能を提供しております。）